Some time ago Chris Schwarz of Lost Art Press mentioned an old-school tradesman trick for eyeballing the standard bevel angle on a plane or chisel blade. Basically, if the bevel face looked to be twice the length of the thickness of the blade, then the bevel angle would equal 30 degrees. If the bevel face looked longer, than the angle would be closer to 25 degrees. (Either angle works, by the way–though some say a steeper angle keeps sharper longer, and might be preferable for A2 steel). In the above photo, the bevel measures out to about 25/64ths.

The thickness of the blade next to the bevel comes to 11/64ths–which is less than half the length of the bevel. So the bevel angle is less than 30 degrees, probably close to the typical 25 degrees. Out of curiosity, let’s see how a quick bit of artisan/intuitive geometry reveals why a 30 degree bevel produces a length exactly twice that of the thickness of the blade:
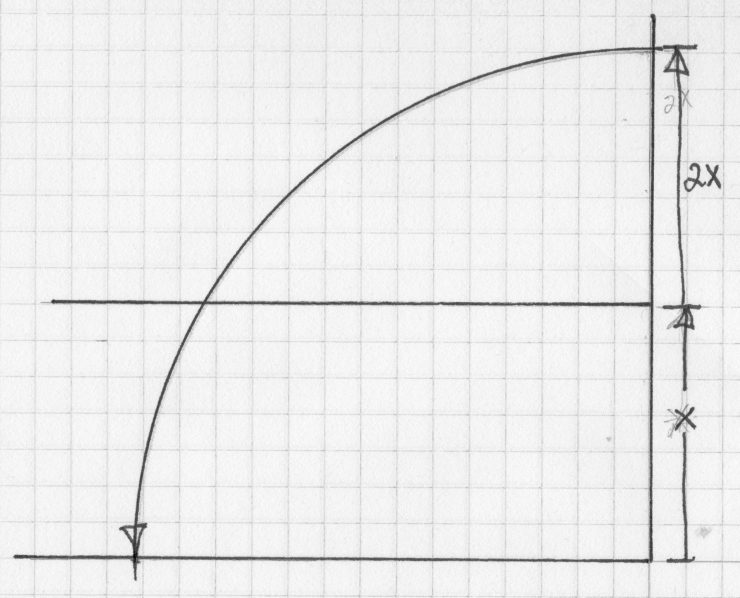
On a piece of graph paper erect a right angle and draw a quadrant of a circle. Divide the radius in half–this represents the thickness of the blade and is indicated by the “X”.
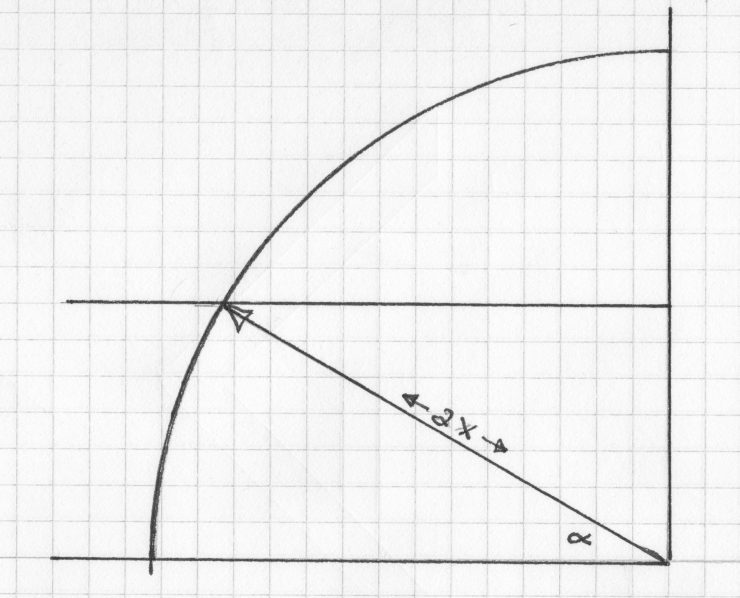
Now connect a line as shown (the line is the radius length–which represents twice the thickness of the “blade”.)
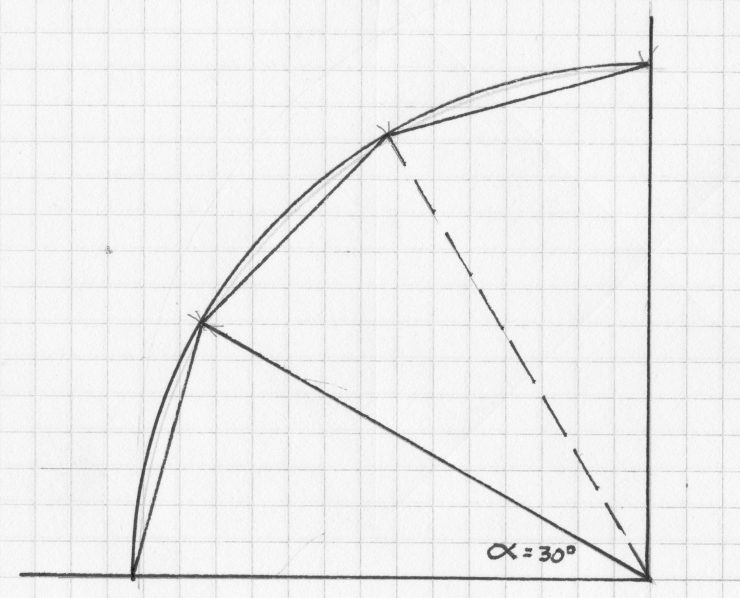
Finally, set your dividers to the marked angle and step around the quadrant. You’ll discover that it steps exactly three times to reach the perpendicular. Which means the angle is describing one-third of the quadrant, and therefore one-twelfth of a full circle. If you divide 360 degrees by 12 you come up with 30 degrees. Of course, you could always just look up the answer in a trig table, but what fun is that?



