Thales of Miletus
In one of the recent posts we showed you how to get a right angle out of a circle, thanks to this guy. A curious reader mentioned it would be interesting to see the proof. Well you can prove this theorem using trig or algebra–the operative word here being you. I’ve long since forgotten how to work these in any reasonable amount of time. Instead, here’s the way an artisan could do it using a simple geometric construction:
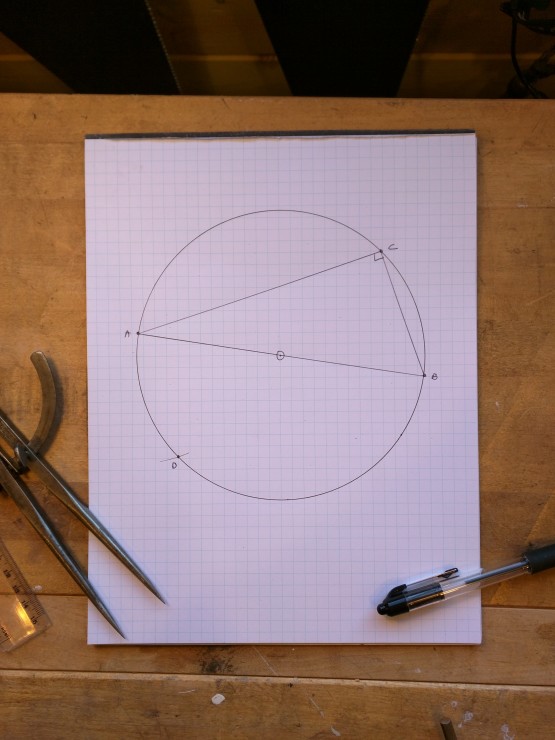
After creating the right triangle above the diameter line AB, make a mirror of this triangle below the line by transferring the leg BC (via your dividers) to establish point D.
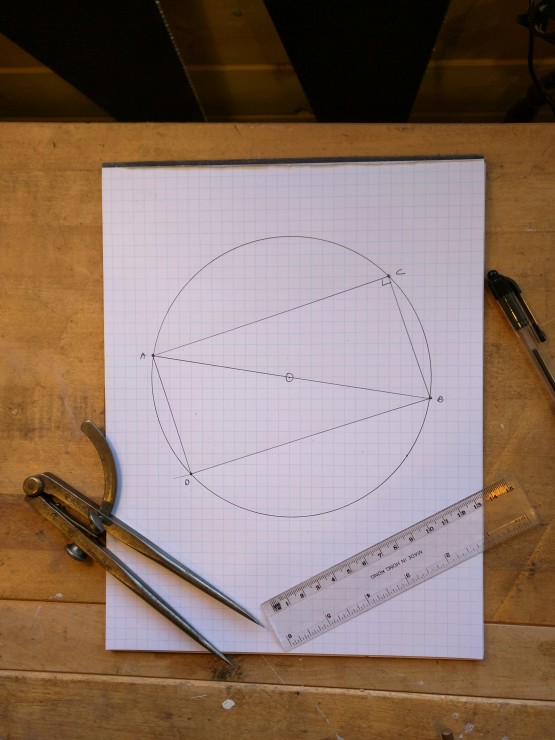
Complete the triangle ADB.
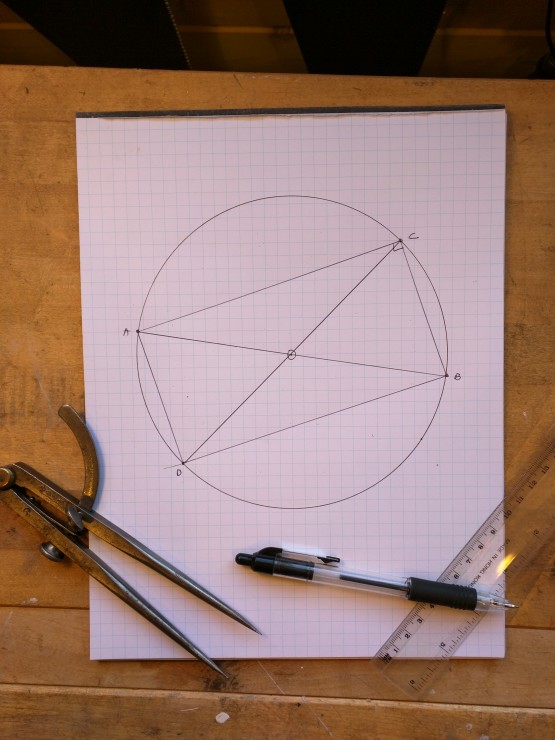
Now draw in a second diameter line (CD). Because the two diameters are obviously the same length, and because the other legs are equal to each other (short = short; long = long) this construction is a rectangle: a polygon with four sides meeting at right angle. No matter where C and D occur opposite each other on the rim of the circle, they will always produce this figure. That’s proof enough for this carpenter!




3 thoughts on “Thales Theorem Proof”
jbaker4041
Very nice! I’ve spent the last day remembering algebra and geometry from 50 years ago, here is what I came up with…
Rule: The angle between the baselines of the triangles created by any diameter of a circle and any other radius is always 90 degrees.
The sum of the apex angles (x and y) of the two triangles equals 180 degrees (since diameter is straight line).
The two triangles are isosceles, with legs equal to the radius, so opposing angles (a and b) are equal in each triangle.
Sum of apex and opposing angles of each triangle is 180 degrees. So sum of two triangles is 360 degrees.
Bases meet at angle equal to sum of one opposing angle from each triangle
Math is:
X + 2a + Y + 2b = 360 subtract x+y = 180
2a + 2b = 180 divide by 2
a + b = 90
Example: make one of the triangles equilateral. All three angles are 60 degrees. The other apex must then be 120 degrees and the opposing angles must be 30 degrees each. 60 plus 30 equals 90 degrees.
jbaker4041
Wow, comparing the two proofs… you win!
keithmitchell
Thanks for digging up such excellent info, and translating it to something I can understand. As someone who always loved drawing and geometry, but not algebra, this really helps a lot.